[This post is based on the paper, “A Primer on the ‘Reproducibility Crisis’ and Ways to Fix It” by the author]

In a previous post, I argued that lowering α from 0.05 to 0.005, as advocated by Benjamin et al. (2017) – henceforth B72 for the 72 coauthors on the paper, would do little to improve science’s reproducibility problem. Among other things, B72 argue that reducing α to 0.005 would reduce the “false positive rate” (FPR). A lower FPR would make it more likely that significant estimates in the literature represented real results. This, in turn, should result in a higher rate of reproducibility, directly addressing science’s reproducibility crisis. However, B72’s analysis ignores the role of publication bias; i.e., the preference of journals and researchers to report statistically significant results. As my previous post demonstrated, incorporating reasonable parameters for publication bias nullifies the FPR benefits of reducing α.

What, then, can be done to improve reproducibility? In this post, I return to B72’s FPR framework to demonstrate that replications offer much promise. In fact, a single replication has a sizeable effect on the FPR over a wide variety of parameter values.

Let α and β represent the rates of Type I and Type II error associated with a 5 percent significance level, with Power accordingly being given by (1-β).  Let ϕ be the prior probability that H₀ is true. Consider a large number of “similar” studies, all exploring possible relationships between different x’s and y’s. Some of these relationships will really exist in the population, and some will not. ϕ is the probability that a randomly chosen study estimates a relationship where none really exists. ϕ is usefully transformed to Prior Odds, defined as Pr(H₁)/Pr(H₀) = (1- ϕ)/ϕ, where H₁ and H₀ correspond to the hypotheses that a real relationship exists and does not exist, respectively. B72 posit the following range of Prior Odds values as plausible for real-life research scenarios: (i) 1:40, (ii) 1:10, and (iii) 1:5.

We are now in position to define the False Positive Rate. Let ϕα be the probability that no relationship exists but Type I error nevertheless produces a significant finding. Let (1-ϕ)(1-β) be the probability that a relationship exists and the study has sufficient power to identify it. The percent of significant estimates in published studies for which there is no underlying, real relationship is thus given by

(1) False Positive Rate(FPR) = ϕα / [ϕα +(1-ϕ)(1-β)] .

Table 1 reports FPR values for different Prior Odds and Power values when α = 0.05.  The FPR values in the table range from 0.24 to 0.91. For example, given 1:10 odds that a studied effect is real, and assuming studies have Power equal to 0.50 – the same Power value that Christensen and Miguel (2017) assume in their analysis – the probability that a statistically significant finding is really a false positive is 50%. Alternatively, if we take a Power value of 0.20, which is about equal to the value that Ioannidis et al. (2017) report as the median value for empirical research in economics, the FPR rises to 71%.

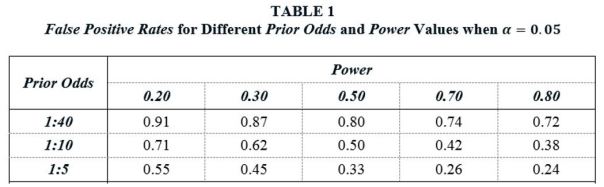
Table 1 illustrates the reproducibility problem highlighted by B72. The combination of (i) many thousands of researchers searching for significant relationships, (ii) relatively small odds that any given study is estimating a relationship that really exists, and (iii) a 5% Type I error rate, results in the published literature reporting a large number of false positives, even without adding in publication bias. In particular, for reasonable parameter values, it is very plausible that over half of all published, statistically significant estimates represent null effects.

I use this framework to show what a difference a single replication can make. The FPR values in Table 1 present the updated probabilities (starting from ϕ) that an estimated relationship represents a true null effect after an original study is published that reports a significant finding. I call these “Initial FPR” values. Replication allows a further updating, with the new, updated probabilities depending on whether the replication is successful or unsucessful. These new, updated probabilities are given below.

(2a) Updated FPR(Replication Successful) ) = InitialFPR∙α / [InitialFPR∙α +(1-InitialFPR)∙(1-β)] .

(2b) Updated FPR(Replication Unsuccessful) ) = InitiailFPR∙(1-α) / [InitialFPR∙(1-α) +(1-InitialFPR)∙β] .

Table 2 reports the Updated FPR values, depending on whether a replication is successful or unsuccessful, with Initial FPR values roughly based on the values in Table 1. Note that Power refers to the power of the replication studies.

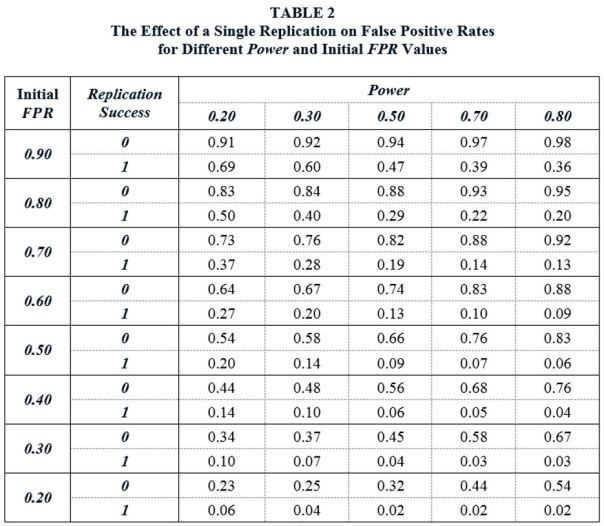
The Updated FPR values show what a difference a single replication can make. Suppose that the Initial FPR following the publication of a significant finding in the literature is 50%. A replication study is conducted using independent data drawn from the same population. If we assume the replication study has Power equal to 0.50, and if the replication fails to reproduce the significant finding of the original study, the FPR increases from 50% to 66%. However, if the replication study successfully replicates the original study, the FPR falls to 9%. In other words, following the replication, there is now a 91% probability that the finding represent a real effect in the population.

Table 2 demonstrates that replications have a sizeable effect on FPRs across a wide range of Power and Initial FPR values. In some cases, the effect is dramatic. For example, consider the case (Initial FPR = 0.80, Power = 0.80). In this case, a single, successful replication lowers the false positive rate from 80% to 20%.  As would be expected, the effects are largest for high-powered replication studies. But the effects are sizeable even when replication studies have relatively low power. For example, given (Initial FPR = 0.80, Power = 0.20), a successful replication lowers the FPR from 80% to 50%.

Up to now, we have ignored the role of publication bias. As noted above, publication bias greatly affects the FPR analysis of B72.  One might similarly ask how publication bias affects the analysis above. If we assume that publication bias is, in the words of Maniadis et al. (2017) “adversarial” – that is, the journals are more likely to publish a replication study if it can be shown to refute an original study – then it turns out that publication bias has virtually no effect on the values in Table 2.

This is most easily seen if we introduce publication bias to Equation (2a) above. Following Maniadis et al. (2017), let ω represent the decreased probability that a replication study reports a significant finding due to adversarial publication bias. Then if the probability of obtaining a significant finding given no real effect is InitialFPR∙α in the absence of publication bias, the associated probability with publication bias will be InitialFPR∙α∙(1-ω). Likewise, if the probability of obtaining a significant finding when a real effect exists is (1-InitialFPR)∙(1-β) in the absence of publication bias, the associated probability with publication bias will be (1-InitialFPR)∙(1-β)∙(1-ω). It follows that the Updated FPR from a successful replication given adversarial publication bias is given by

(3) Updated FPR(Replication Successful|Adversarial Publication Bias) = FPR∙α∙(1-ω) / [FPR∙α∙(1-ω) +(1-FPR)∙(1-β)∙(1-ω)] .

Note that the publication bias term in Equation (3), (1-ω), cancels out from the numerator and denominator, so that the Updated FPR in the event of a successful replication is unaffected. The calculation for unsuccessful replications is not quite as straightforward, but the result is very similar: the Updated FPR is little changed by the introduction of adversarial publication bias.

It needs to be pointed out that the analysis above refers to a special type of replication, one which reproduces the experimental conditions (data preparation, analytical procedures, etc.) of the original study, albeit using independent data drawn from an identical population. In fact, there are many types of replications. Figure 1 (see below) from Reed (2017) presents six different types of replications. The analysis above clearly does not apply to some of these.

For example, Power is an irrelevant concept in a Type 1 replication study, since this type of replication (“Reproduction”) is nothing more than a checking exercise to ensure that numbers are correctly calculated and reported. The FPR calculations above are most appropriate for Type 3 replications, where identical procedures are applied to data drawn from the same population as the original study. The further replications deviate from a Type 3 model, the less applicable are the associated FPR values. Even so, the numbers in Table 2 are useful for illustrating the potential for replication to substantially alter the probability that a significant estimate represents a true relationship.

There is much debate about how to improve reproducibility in science. Pre-registration of research, publishing null findings, “badges” for data and code sharing, and results-free review have all received much attention in this debate. All of these deserve support. While replications have also received attention, this has not translated into a dramatic increase in the number of published replication studies (see here). The analysis above suggests that maybe, when it comes to replications, we should take a lead from the title of that country-western classic: “A Little Less Talk And A Lot More Action”.

Of course, all of the above ignores the debate around whether null hypothesis significance testing is an appropriate procedure for determining “replication success.” But that is a topic for another day.

REFERENCES

Benjamin, D.J., Berger, J.O., Johannesson, M. Nosek, B.A., Wagenmakers, E.-J., Berk, R., …, Johnson, V.E. (2017). Redefine statistical significance. Nature Human Behaviour, 1(0189).

Christensen, G.S. and Miguel, E. (2016). Transparency, reproducibility, and the credibility of economics research. CEGA Working Paper Series No. WPS-065. Center for Effective Global Action. University of California, Berkeley.

Ioannidis, J.P., Doucouliagos, H. and Stanley, T. (2017). The power of bias in economics. Economic Journal 127(605): F236-65.

Maniadis, Z., Tufano, F., and List, J.A. (2017). To replicate or not to replicate? Exploring reproducibility in economics through the lens of a model and a pilot study. Economic Journal, 127(605): F209-F235.

Reed, W.R. (2017). A primer on the “reproducibility crisis” and ways to fix it. Working Paper No. 21/2017, Department of Economics and Finance, University of Canterbury, New Zealand.