The Replication Network
Furthering the Practice of Replication in Economics
REED: Using the Stata Package “speccurve” to Do Specification Curve Analysis
NOTE: The data (“COUPE.dta”) and code (“speccurve_program.do”) used for this blog can be found here: https://osf.io/4yrxs/
In a previous post (see here), I provided a step-by-step procedure for using the R package “specr”. The specific application was reproducing the specification curve analysis from a paper by Tom Coupé and coauthors (see here).
“speccurve”
In this post, I do the same, only this time using the Stata program “speccurve” (Andresen, 2020). The goal is to facilitate Stata users to produce their own specification curve analyses. In what follows, I presume the reader has read my previous post so that I can go straight into the code.
The first step is to download and install the Stata program “speccurve” from GitHub:
There isn’t a lot of documentation for “speccurve.” The associated GitHub site includes an .ado file that provides examples (“speccurve_gendata.ado”). Another example is provided by this independent site (though ignore the bit about factor variables, as that is now outdated).
“speccurve” does not do everything that “specr” does, but it will allow us to produce versions of FIGURE 1 and TABLE 1. (Also, FIGURE 2, though for large numbers of specifications, the output isn’t useful.)
What “speccurve” Can Do
Here is the “speccurve” version of FIGURE 1 from my previous post:
And here are the results for TABLE 1:
How about FIGURE2? Ummm, not so helpful (see below). I will explain later.
Unlike “specr”, “speccurve” does not automatically create combinations of model features for you. You have to create your own. “speccurve” is primarily a function for plotting a specification curve after you have estimated your selected specifications. The latter is typically done by creating a series of for loops.
Downloading Data and Code, Setting the Working Directory, Reading in the Data
Once you have installed “speccurve”, the next step is to create a folder, download the the dataset “COUPE.dta” and code “speccurve_program.do” from the OSF website (here), and store them in the folder. COUPE.dta is a Stata version of the COUPE.RData dataset described in the previous post.
The following section provides an explanation for each line of code in “speccurve_program.do”.
The command line below sets the working directory equal to the folder where the data are stored.
The next step clears the working memory.
“speccurve” stores results in a “.ster” file. If you have previously run the program and created a “.ster” file, it is good practice to remove it before you run the program again. In this example, I have called the .ster file “WarSatisfaction”. To remove this file, delete the comment markers from the second line of code below and run.
Now import the Stata dataset “COUPE”.
Making Variables for the For Loops
Recall from the previous post that Coupé created 320 specifications by combining the following model characteristics: (i) two dependent variables, (ii) four samples, (iii) eight variables, and (iv) five models. Many of these had cumbersome names. Since I will reproduce Coupé’s specifications using for loops, I want to simplify the respective names.
For example, rather than referring to “lifesatisfaction15” and “lifesatisfaction110”, I create duplicate variables and name them “y1” and “y2”. Likewise, I create and name four sample variables, “sample1” to “sample4”.
Having done this for “y” and “sample”, I now want to do the same thing for the different variable specifications. There were eight variable combinations. I create a “local macro” for each one, associating the names “var1” to “var8” with specific sets of variables.
For example, “var1” refers to the set of variables that Coupé collectively referred to “No Additional Controls”.
“var2” refers to the set of variables Coupé called “Other Controls”.
In this way, all eight of the variable sets receive “shorthand” names “var1” to “var8”.
A For Loop for All the Djankovetal2016 Specifications
We now get to the heart of the program. I create another local macro called “no” that will assign a number (= “no”) to each of the models I estimate (model1-model320). I initialize “no” at “1”.
I write separate for loops for each of the five models, starting with Djankovetal2016.
I set up three levels of for loops. Starting from the outside (top), there are four types of samples (sample1-sample4), two types of dependent variables (y1-y2) and eight variable sets (var1-var8).
Djankovetal2016 estimates a weighted, linear regression model without fixed effects so I reproduce that estimation approach here. Note how “i”, “j”, and “k” allow different combinations of variables, dependent variables, and samples, respectively.
The next lines of commands identify which model we are estimating. The “estadd” command creates a variable that assigns either a “1” or a “0” depending on the model. Since the first model is Djankovetal2016, Model1 = 1 and all the other Model variables (Model2-Model5) are set = 0. ”estadd” saves the model variables so that we can identify the estimation model that each specification uses.
I next do the same thing for variable sets. Recall that the “i” indicator loops through eight variable specifications. When “i” = 1, the variable “Vars1” takes the value 1. When “i” = 2, the variable “Vars2” takes the value 1. And so on.
Having set the “right” Vars variable to “1”, I then set all the other Vars variables to “0”. That’s what the next set of commands do.
If “i” is not equal to 1, then Vars1 = 0. If “i” is not equal to 2, then Vars2 = 0. At the end of this section, all the Vars variables have been set = 0 except for the one variable combination that is being used in that regression.
I next do the exact same thing for the dependent variable, Y. “j” takes the values “1” or “2” depending on which dependent variable is being used. When “j” = 1, Y1 = 1. When “j” = 2, Y2 = 1. The remaining lines set Y2 = 0 or Y1 = 0 depending if “j” = 1 or 2, respectively.
And then the same thing for the sample variables.
The next two lines save the results in a (“.ster”) file called “WarSatisfaction” and assigns each set of results a unique model number (“model1”-“model320”).
The last few lines of this for loop increases the “no” count by 1, and then the three right hand brackets finish off the three levels of the for loop.
For Loops for the Other 4 Estimation Models
Having estimated all the specifications associated with the Djankovetal2016 model, I proceed similarly for the other four estimation models.
Producing the Specification Curve
After running all 320 model specifications and storing them in the file “WarSatisfaction”, the “speccurve” command below produces the sought-after specification curve.
The option “param” lets “speccurve” know which coefficient estimate it should use. “title” is the name given to the figure produced by “speccurve”. “panel” produces the box below the figure (see below), the analogue of FIGURE 2 in the “specr” post.
Ideally, the panel sits below the specification curve and identifies the specific model characteristics that are associated with each of the 320 estimates. However, with so many specifications, it is squished down to an illegible box . If the reader finds this annoying, they can safely omit the “panel’ option.
Producing the Regression Results for TABLE 1
To produce TABLE 1, we need to access a table that is automatically produced by “speccurve” and stored in a matrix called “r(table)”. The following command prints out “r(table)” for inspection.
“r(table)” stores variables for each of the 320 model specifications estimated by “speccurve”. The first two stored variables are “modelno” and “specno”. We saw how “modelno” was created in the for loops above. “specno” simply sorts the models so that the model with the lowest estimate is “spec1” and the model with the largest is “spec320).
Then comes “estimate”, “min95”, “max95”, “min90”, and “max90”. These are the estimated coefficients for the war “treatment variable”, and the respective 95- and 90-confidence interval limits.
After these is a series of binary variables (“Model1”-“Model5”, “Vars1”-“Vars8”, “Y1”-“Y2”, and “Sample1”-“Sample4”) that identify the specific characteristics associated with each estimated model.
With the goal of producing TABLE 1, I next turn this matrix into a Stata dataset. The following command takes the variables stored in the matrix “r(table)” and adds them to the existing COUPE.dta dataset, giving them the same names they have in “r(table)”.
With these additions, the COUPE.dta dataset now consists of 38,843 observations and 90 variables, 26 more variables than before because of the addition of the “r(table)” variables.
I want to isolate these “r(table)” variables in order to estimate the regression of TABLE 1. To do that, I run the following lines of code:
Now the only observations and variables in Stata’s memory are the data from “r(table)”. I could run the regression now, regressing “estimate” on the respective model characteristics. However, matching variable names like “Model 1” and “Vars7” to the variable names that Coupé uses in his TABLE 1 is inconvenient and potentially confusing.
Instead, I want to produce a regression table that looks just like Coupé’s. To do that, I install a Stata package called “estout” (see below).
“estout” provides the option of reporting labels rather than variable names. To take advantage of that, I next assign a label to each of the model characteristic variable names.
Now I am finally in a position to estimate and report TABLE 1.
First, I regress the variable “estimate” on the respective model characteristics. To match Coupé’s table, I set the reference category equal to Model5=1, Sample4 = 1, Vars8=1, and Y2=1 and omit these from the regression.
Next I call up the command “esttab”, part of “estout”, and take advantage of the “label” option that replaces variable names with their labels.
“varwidth” formats the output table to look like Coupé’s TABLE 1. Likewise, “order” puts the variables in the same order as Coupé’s table. “se” has the table report standard errors rather than t-statistics, and b(%9.3f) reports coefficient estimates and standard errors to three decimal places, again to match Coupé’s table.
And voilá, we’re done! You can check that the resulting TABLE 1 exactly matches Coupé’s table by comparing it with TABLE 1 from the previous “specr” post.
Saving the Results
As a final action, you may want to save the table as a WORD doc for later editing. This can be done by inserting “using TABLE1.doc” (or whatever you want to call it) after “esttab” but before the comma in the command line above.
One could also save the “speccurve” dataset for later analysis using the “save” command, as below, where I have called it “speccurve_output”. This is saved as a standard .dta Stata dataset.
Conclusion
You are now all set to use Stata to reproduce the results from Coupé’s paper. Go to the OSF site given at the top of this blog, download the data and code, and run the code to produce the results in this blog. It took about 7 minutes to run on my laptop.
Of course the goal is not to just reproduce Coupé’s results, but rather to prepare you to do your own specification curve analyses. As noted above, for more examples, go to the “speccurve” GitHub site and check out “speccurve_gendata.ado”. Good luck!
NOTE: Bob Reed is Professor of Economics and the Director of UCMeta at the University of Canterbury. He can be reached at bob.reed@canterbury.ac.nz. Special thanks go to Martin Andresen for his patient assistance in answering Bob’s many questions about “speccurve”.
REFERENCES
Andresen, M. (2020). martin-andresen/speccurve [Software]. GitHub. https://github.com/martin-andresen/speccurve
REED: Using the R Package “specr” To Do Specification Curve Analysis
NOTE: The data (“COUPE.Rdata”) and code (“specr_code.R”) used for this blog can be found here: https://osf.io/e8mcf/
A Tutorial on “specr”
In a recent post, Tom Coupé encouraged readers to create specification curves to represent the robustness of their results (or lack thereof). He illustrated how this could be done using the R package “specr” (Masur & Scharkow. 2020).
In this blog, I provide instructions that allow one to reproduce Coupé’s results using a modified version of his code. In providing a line-by-line explanation of the code that reproduces Coupe’s results, it is hoped that the reader will have sufficient understanding to enable them to use the “specr” package for their own applications. Later, in a follow-up blog, I will do the same using Stata’s “speccurve” program.
Specification Curve Analysis
Specification curve analysis (Simonsohn, Simmons & Nelson, 2020), also known as multiverse analysis (Steegen et al., 2016) is used to investigate the “garden of forking paths” inherent in empirical analysis. As everyone knows, there is rarely a single, best way to estimate the relationship between a dependent variable y and a causal or treatment variable x. Researchers can disagree about the estimation procedure, control variables, samples, and even the specific variables to best represent the treatment and the outcome of interest.
When the list of equally plausible alternatives (Del Giudice & Gangestad, 2021) is relatively short, it is an easy task to estimate, and report, all alternatives. But suppose the list of equally plausible alternatives is long? What can one do then?
Specification curve analysis provides a way of estimating all reasonable alternatives and presenting the results in a way that makes it easy to determine the robustness of one’s conclusions.
The Coupé Study
In Coupé’s post, he studied five published articles, all of which investigated the long-term impact of war on life satisfaction. Despite using the same dataset (the “Life in Transition Survey” dataset), the five articles came to different conclusions about both the sign and statistical significance of the relationship between war and life satisfaction.
Complicating their interpretation, the five studies used different estimation methods, different samples, different measures of life satisfaction, and different sets of control variables. Based on these five studies, Coupé identified 320 plausible alternatives. He then produced the following specification curve.
FIGURE 1 sorts the estimates from lowest to highest. Point estimates are indicated by dots, and around each dot is a 95% confidence interval. Red dots/intervals indicate the point estimate is statistically significant. Grey dots/ intervals indicate statistical insignificance.
This specification curve vividly demonstrates the range of point estimates and statistical significances that are possible depending on the combination of specification characteristics. One clearly sees three sets of results: negative and significant, negative and insignificant, and positive and insignificant.
“specr” also comes with a feature that allows one to connect results to specific combinations of specification characteristics.
FIGURE 2 identifies the individual specification characteristics: There is one “x” variable (“WW2injury”). There are two “y” variables (“lifesatisfaction15” and “lifesatisfaction110”). There are five general estimation models corresponding to the five studies (“NikolovaSanfey2016”, “Kjewski2020”, “Ivlevs2015”, “Djankoveta2016”, and “ChildsNikolova2020”). There are 8 possible combinations of the variable sets “War Controls”, “Income”, and “Other Controls”. And there are four possible samples. This yields 1x2x5x8x4 = 320 model specifications.
The figure allows one to visually connect results to characteristics, with red (blue) markers indicating significant (insignificant) estimates, and estimates increasing in size as one moves from left to right in the figure. However, to investigate further, one needs to do a proper multivariate analysis.
Coupé chose to do this by estimating a linear regression, establishing one specification as the reference category and representing the other model characteristics with dummy variables. The reference case was defined as Model = ChildsNikolova2020, Subset = All, Controls = Income controls, and Dependent Variable = lifesatisfaction110.[1]
Because the model covariates are all dummy variables, the estimated coefficients can be directly compared. From TABLE 1 below (which is Table III in Coupé’s paper) we observe that specifications that include “Income Controls” are associated with larger (less negative, more positive) estimates of the effect of war injury on life satisfaction.
Using “specr”
Now that we know what specification curve analysis can do, the next step is to go over the code that produced these results. The following provides line-by-line explanations of the code (provided here) used to reproduce the two figures and the table above.
First, create a folder and place the dataset COUPE.RData in it. COUPE.RData is a dataset that I created using datasets from Coupé’s github site (see here).
Open R and start a new script by setting the working directory equal to that folder.
Use the library command to read in all the packages you need to run the program. Install any packages that you do not currently have installed.
The following command discourages R from reporting results using scientific notation.
Now we read in the dataset, COUPE, an R dataset.
The “setup” command
The heart of the “specr” package is the “setup” command. It lays out the individual components that will combined to produce a given specification. The syntax for the “setup” command is given below (documentation here):
It involves specifying the dataset, the treatment variable(s) (“x”), the dependent variable(s) (“y”), the sets of control variables (“controls”), and the different subsets (“subsets”). The “add_to_formula” option identifies a constant set of control variables that are included in every specification.
You will have noticed that I skipped over “model”. This is where the different estimation procedures are identified. In Coupé’s analysis, he specified five different models, each representing one of the five papers in his study. This is the most complicated part of the “setup” command, which is why I saved it for last.
Coupé named each of his models after the paper they represents. Here is how the model for Kijewski2020 is defined:
Kijewski2020 is a customized function that has three components. “formula” is defined by the combination of characteristics that define a particular specification. “data” is the dataset identified in the “setup” command, and the third line indicates that Kijewski2020 used a two-level, mixed effects models. To estimate this model, Coupé uses the R function “lmer”. The only twist here is the addition of “+(1|country)” that lets “lmer” know to include random effects at the country level.
The other studies are represented similarly. Below is how the model for ChildsNikolova2020 is defined:
Rather than estimating a multi-level model, ChildsNikolova2020 estimates a fixed effects, OLS model. The component “|Region1” adds regional dummy variables to the variable specification. The “cluster” and “weights” options compute cluster robust standard errors (CR1-type) and allow for weighting, designed to give each country in the sample an equal weight.
The other models are defined similarly.
Having defined the individual models, we can now assemble the individual specification components in the “setup” command.
The first several lines should be easy to interpret, having been discussed above. “subset” identifies two subsets: “sample15” = “Heavily affected countries only”; “under65” = “Under sixty-five”. “specr” turns this into four samples: (i) “sample15”, (ii) under65”, (iii) “sample15” & “under65”, and (iv) the full sample (“all”).
“controls” identifies three sets of controls. I have separated the three sets of controls to make them easier to identify. The first is what Coupé calls “Other controls”. The second is what he calls “War controls”; and the third, “Income Controls”. In combination with the option “simplify = FALSE”, “specr” turns this into 8 sets of control variables, which is equal to all possible combinations of the three sets of control variables (none, each individually, each combination between each variable, all variables). If simplify = TRUE”, had been selected, only five sets of control variables would have been included (no covariates, each individually, and all covariates).
The last element in “setup” command is “add_to_formula”. This identifies variables that are common to every specification. This option allows one to list these variables once, rather than repeating the list for each set of control variables.
FIGURE 1
Together, the “setup” command creates an object called “specs”. In turn, “specr” takes this object and creates another object, “results”, which is then fed into subsequent “specr” functions.
And just like that, we can now use the command “plot” to produce our specification curve.
FIGURE 2
Moving on to FIGURE 2, the next set of six commands renames the respective sets of control variables and sample subsets for more convenient representation in subsequent outputs. As it is not central to running “specr”, but is only done to make the output more legible, I will only give a cursory explanation.
The “specr” command produces an object called “results$data” (see below). Inside it are contained many columns, including “x”, “y”, “model”, “controls”, “subsets”, etc. It has 320 rows, with each row containing details about the respective model specifications.
“results$data$controls” reports the variables used for each of the model specifications. Each of the six renaming commands replaces the contents of “controls” with shorter descriptions.
For example, the command below creates a temporary dataset called “tom” which is a copy of “results$data$controls”.
It looks for the text in the 10th row of “tom”, tom[10] = “recentwarmoved+recentwarinjury+recentwarHHinjury+ WW2moved”. Every time it sees that text in “tom” it replaces it with “War Controls”. It then substitutes “tom” back into “results$data$controls”.
The other five renaming commands all do something similar.
With the variable names cleaned up for legibility, we’re ready to produce FIGURE 2.
TABLE 1
The last task is to produce TABLE 1. The estimates in TABLE 1 come from a standard OLS regression, which we again call “tom” (I don’t know where Coupé comes up with these names!).
The only thing unusual about this regression is that the dependent variable “estimate” and the explanatory variables (“model”, “subsets”, etc.) come from the dataset “results$data” described above.
We could have printed out the regression results from “tom” using the familiar “summary” command, but the output is very messy and hard to read.
Instead, we take the regression results from “tom” and use the “stargazer” package to create an attractive table. Note, however, we had to first look at the regression results from “tom” to get the correct order for naming the respective factor variables.
You can now go to the OSF site given at the top of this blog, download the data and code there, and produce the results in this blog (and Coupé’s paper). That should enable you to do your own specification curve analysis.
To learn more about “specr”, and see some more examples, go here.
NOTE: Bob Reed is Professor of Economics and the Director of UCMeta at the University of Canterbury. He can be reached at bob.reed@canterbury.ac.nz.
[1] Personally, I would have omitted the constant term and included all the model characteristics as dummy variables.
REFERENCES
Del Giudice, M., & Gangestad, S. W. (2021). A traveler’s guide to the multiverse: Promises, pitfalls, and a framework for the evaluation of analytic decisions. Advances in Methods and Practices in Psychological Science, 4(1), 1-15.
Masur, Philipp K., and Michael Scharkow. 2020. “Specr: Conducting and Visualizing Specification Curve Analyses (Version 1.0.1).” https://CRAN.R-project.org/package=specr.
Simonsohn, U., Simmons, J. P., & Nelson, L. D. (2020). Specification curve analysis. Nature Human Behaviour, 4(11), 1208-1214.
Steegen, S., Tuerlinckx, F., Gelman, A., & Vanpaemel, W. (2016). Increasing transparency through a multiverse analysis. Perspectives on Psychological Science, 11(5), 702-712.
REED & LOGCHIES: Calculating Power After Estimation – No Programming Necessary!
Introduction. Your analysis produces a statistically insignificant estimate. Is it because the effect is negligibly different from zero? Or because your research design does not have sufficient power to achieve statistical significance? Alternatively, you read that “The median statistical power [in empirical economics] is 18%, or less” (Ioannidis et al., 2017) and you wonder if the article you are reading also has low statistical power. By the end of this blog, you will be able to easily answer both questions. Without doing any programming.
An Online App. In this post, we show how to calculate statistical power post-estimation for those who are not familiar with R. To do that, we have created a Shiny App that does all the necessary calculating for the researcher (CLICK HERE). We first demonstrate how to use the online app and then showcase its usefulness.
How it Works. The input window requires researchers to enter four numbers: (i) The alpha value corresponding to a two-tailed test of significance; (ii) the degrees of freedom of the regression equation; (iii) the standard error of the estimated effect; and (iv) the effect size for which the researcher wants to know the corresponding statistical power.
The input window comes pre-filled with four values to guide how researchers should enter their information. (The numbers in the table are taken from an example featured in the previous TRN blog). Once the respective information is entered, one presses the “Submit” button.
The app produces two outputs. The first is an estimate of statistical power that corresponds to the “Effect size” entered by the researcher. For example, for the numbers in the input window above, the app reports the following result: “Post hoc power corresponding to an effect size of 4, a standard error of 1.5, and df of 50 = 74.3%” (see below).
In words, this regression had a 74.3% probability of producing a statistically significant (5%, two-tailed) coefficient estimate if the true effect size was 4.
The second output is a power curve (see below).
The power curve illustrates how power changes with effect size. When the effect size is close to zero, it is unlikely that the regression will produce a statistically significant estimate. When the effect size becomes large, the probability increases, eventually asymptoting to 100%.
The power curve plot also includes two vertical lines: “Effect size” and “80% power”. The former translates the “Calculation Result” from above and places it within the plot area. The latter plots the effect size that corresponds to 80% power as a reference point.
Useful when Estimates are Statistically Insignificant. One application of post-hoc power is that it can help distinguish when statistical insignificance is due to a negligible effect size versus when it is the result of a poorly powered research design.
Tian et al. (2024), on which this blog is based, give the example of a randomized controlled trial that was designed to have 80% power for an effect size of 0.060, where 0.060 was deemed sufficiently large to represent a meaningful economic effect. Despite estimating an effect of 0.077, the study found that the estimated effect was statistically insignificant (degrees of freedom = 62). In fact, the power of the research design as it was actually implemented was only 20.7%.
We can illustrate this case in our online app. First, we enter the respective information in the input window:
This produces the following “Calculation Result”,
and associated Power Curve:
As it was implemented, the estimated regression model only had a 20.7% probability of producing a statistically significant estimate for an effect size (0.060) that was economically meaningful. Clearly, it would be wrong to interpret statistical insignificance in this case as indicating that the true effect was negligible.
How About When it is Difficult to Interpret Effect Sizes? The example above illustrates the case where it is straightforward to determine an economically meaningful effect size for calculating power. When it is not possible to do this, the online Post Hoc Power app can still be of use by converting estimates to “partial correlation coefficients” (PCCs).
PCCs are commonly used in meta-analyses to convert regression coefficients to a common effect size. All one needs is the estimated t-statistic and the regression equation’s degrees of freedom (df):
The advantage of converting regression coefficients to PCCs is that there exist guidelines for interpreting the associated economic sizes of the effects. First, though, we demonstrate how converting the previous example to a PCC leads to a very similar result.
To get the t-statistics for the previous example, we divide the estimated effect (0.077) by its standard error (0.051) to obtain t = 1.176. Given df = 62, we obtain PCC = 0.148 and se(PCC) = 0.124. We input these parameter values into the input window (see below).
The output follows below:
A comparison of FIGURES 3B and 2B and FIGURES 3C and 2C confirms that the conversion to PCC has produced very similar power calculations.
Calculating Power for the Most Recent issue of the American Economic Journal: Applied Economics. For our last demonstration of the usefulness of our online app, we investigate statistical power in the most recent issue of the American Economic Journal: Applied Economics (July 2024, Vol. 16, No.3).
There are a total of 16 articles in that issue. For each article, we selected one estimate that represented the main effect. Five of the articles’ did not provide sufficient information to calculate power for their main effects, usually because they clustered standard errors but did not report the number of clusters. That left 11 articles/estimated effects.
To determine statistical power, we converted all the estimates to PCC values and calculated their associated se(PCC) values (see above). We then calculated power for three effect sizes.
To select the effect sizes, we turned to a very useful paper by Chris Doucouliagos entitled “How Large is Large? Preliminary and relative guidelines for interpreting partial correlations in economics”, Doucouliagos collected 22,000 estimated effects from the economics literature and converted them to PCCs. He then rank-ordered them from smallest to largest. Reference points for “small”, “medium” and “large” were set at the 25th, 50th, and 75th percentile values. For the full dataset, the corresponding PCC values were 0.07, 0.17, and 0.33.
Our power analysis will calculate statistical power for these three effect sizes. Specifically, we want to know how much statistical power each of the studies in the most recent issue of the AEJ: Applied Economics had to produce significant estimates for effect sizes corresponding to “small”, “medium”, and “large”. The results are reported in the table below.
We can use this table to answer the question: Are studies in the most recent issue of the AEJ: Applied Economics underpowered? Based on a very limited sample, our answer would be some are, but most are not. The median power of the 11 studies we investigated was 81.8% for a “small” effect. These results differ substantially from what Ioannidis et al. (2017) found. Why the different conclusions? We have some ideas, but they will have to wait for a more comprehensive analysis. However the point of this example was not to challenge Ioannidis et al.’s conclusion. It is merely to show how useful, and easy, calculating post hoc power can be. Everybody should do it!
NOTE: Bob Reed is Professor of Economics and the Director of UCMeta at the University of Canterbury. He can be reached at bob.reed@canterbury.ac.nz. Thomas Logchies is a Master of Commerce (Economics) student at the University of Canterbury. He was responsible for creating the Shiny App for this blog. His email address is thomas.logchies@pg.canterbury.ac.nz .
REFERENCE
REED: Calculating Power After Estimation – Everybody Should Do This!
So your estimate is statistically insignificant and you’re wondering: Is it because the effect size is small, or does my study have too little power? In Tian et al. (2024), we propose a simple method for calculating statistical power after estimation (“post hoc power analysis”). While our application is targeted towards empirical studies in development economics, the method has many uses and is widely applicable across disciplines.
It is common to calculate statistical power before estimation (“a priori power analysis”). This allows researchers to determine the minimum sample size to achieve a given level of power for a given effect size. In contrast, post hoc power analysis is rarely done, and often discouraged (for example, see here).
There is a reason for this. The most common method for calculating post hoc power is flawed. In our paper, we explain the problem and demonstrate that our method successfully avoids this issue.
Before discussing our method, it is useful to review some of the reasons why one would want to calculate statistical power after estimation is completed.
When estimates are insignificant. All too commonly, statistical insignificance is taken as an indication that the true effect size is small, indistinguishable from zero. That may be the case. But it also may be the case that the statistical power of the study was insufficient to generate significance even if the true effect size were substantial. Knowing the statistical power of the regression equation that produced the estimated effect can help disentangle these two cases.
When estimates are significant. Post hoc power analysis can also be useful when estimates are statistically significant. In a recent paper, Ioannidis et al. (2017) analyzed “159 empirical economics literatures that draw upon 64,076 estimates of economic parameters reported in more than 6,700 empirical studies”. They calculated that the “median statistical power is 18%, or less.” Yet the great majority of these estimates were statistically significant. How can that be?
One explanation is Type M error. As elaborated in Gelman and Carlin (2014), Type M error is a phenomenon associated with random sampling . Estimated effects that are statistically significant will tend to be systematically larger than the population effect. If journals filter out insignificant estimates, then the estimates that get published are likely to overestimate the true effects.
Low statistical power is an indicator that Type M error may be present. Post hoc power analysis cannot definitively establish the presence of Type M error. The true effect may be substantially larger than the value assumed in the power analysis. But post hoc power analysis provides additional information that can help the researcher interpret the validity of estimates.
Our paper provide examples from actual randomized controlled trials that illustrate the cases above. We also demonstrate how post hoc power analysis can be useful to funding agencies to assess whether previously funded research met their stated power criteria.
Calculating statistical power. Mathematically, the calculation of statistical power (either a priori or post hoc) is straightforward. Let:
ES = an effect size
s.d.(ES_hat) = the standard deviation of estimated effects, ES_hat
τ = ES / s.d.(ES_hat)
tcritdf,1-α/2 = the critical t-value for a two-tailed t-test having df degrees of freedom and an associated significance level of α.
Given the above, one can use the equation below to calculate the power associated with any effect size ES:
(1) tvaluedf,1-Power = (tcritdf,1-α/2 – τ )
Equation (1) identifies the area of the t-distribution with df degrees of freedom that lies to the right of (tcritdf,1-α/2 – τ) (see FIGURE 1 in Tian et al., 2024). All that is required to calculate power is a given value for the effect size, ES; the standard deviation of estimated effect sizes, s.d.(ES_hat), which will depend on the estimator (e.g., OLS, OLS with clustered standard errors, etc.); the degrees of freedom df and the significance level α.
Most software packages that calculate statistical power essentially consist of estimating s.d.(ES_hat) based on inputs such as sample size, estimate of the standard deviation of the output variable, and other parameters of the estimation environment. This raises the question, why not directly estimate s.d.(ES_hat) with the standard error of the associated regression coefficient?
The SE-ES Method. We show that simply replacing s.d.(ES_hat) with the standard error of the estimated effect from the regression equation, s.e.(ES_hat), produces a useful, post hoc estimator of power. We call our method “SE-ES”, for Standard Error-Effect Size.
As long as s.e.(ES_hat) provides a reliable estimate of the variation in estimated effect sizes, SE-ES estimates of statistical power will perform well. As McKenzie and Ozier (2019) note, this condition generally appears to be the case.
Our paper provides a variety of Monte Carlo experiments to demonstrate the performance of the SE-ES method when (i) errors are independent and homoskedastic, and (ii) when they are clustered.
In the remainder of this blog, I present two simple R programs for calculating power after estimation. The first program produces a single-valued, post hoc estimate of statistical power. The user provides a given effect size, an alpha level, and the standard error of the estimated effect from the regression equation along with its degrees of freedom. This program is given below.
# Function to calculate power
power_function <- function(effect_size, standard_error, df, alpha) {
# This matches FIGURE 1 in Tian et al. (2024)
# "Power to the researchers: Calculating power after estimation"
# Review of Development Economics
# http://doi.org/10.1111/rode.13130
t_crit <- qt(alpha / 2, df, lower.tail = FALSE)
tau <- effect_size / standard_error
t_value = t_crit - tau
calculate_power <- pt(t_value, df, lower.tail = FALSE)
return(calculate_power)
}For example, if after running the power_function above, one wanted to calculate post hoc power for an effect size = 4, given a regression equation with 50 degrees of freedom where the associated coefficient had a standard error of 1.5, one would then run the chunk below.
# Example
alpha <- 0.05
df <- 50
effect_size <- 4
standard_error <- 1.5
power <- power_function(effect_size, standard_error, df, alpha)
print(power)In this case, post hoc power is calculated to be 74.3% (see screen shot below).
Alternatively, rather than calculating a single power value, one might find it more useful to generate a power curve. To do that, you would first run the following program defining two functions: (i) the power_function (same as above), and (ii) the power_curve_function.
# Define the power function
power_function <- function(effect_size, standard_error, df, alpha) {
# Calculate the critical t-value for the upper tail
t_crit <- qt(alpha / 2, df, lower.tail = FALSE)
qt(alpha / 2, df, lower.tail = FALSE)
tau <- effect_size / standard_error
t_value <- t_crit - tau
calculate_power <- pt(t_value, df, lower.tail = FALSE)
return(calculate_power)
}
# Define the power_curve_function
# Note that this uses the power_function above
power_curve_function <- function(max_effect_size, standard_error, df, alpha) {
# Initialize vector to store results
powers <- numeric(51)
# Calculate step size for incrementing effect sizes
d <- max_effect_size / 50
# Create a sequence of 51 effect sizes
# Each incremented by step size d
effect_sizes <- seq(0, max_effect_size, by = d)
# Loop through each effect size to calculate power
for (i in 1:51) {
effect_size <- effect_sizes[i]
power_calculation <- power_function(effect_size, standard_error, df, alpha)
powers[i] <- power_calculation
}
return(data.frame(EffectSize = effect_sizes, Power = powers))
}Now suppose one wanted to create a power curve that corresponded to the previous example. You would still have to set alpha and provide values for df and the standard error from the estimated regression equation. But to generate a curve, you would also have to specify a maximum effect size.
The code below sets a maximum effect size of 10, and then creates a sequence of effect sizes from 0 to 10 in 50 equal steps.
# Define global parameters
alpha <- 0.05
df <- 50
standard_error <- 1.5
max_effect_size <- 10
d <- max_effect_size / 50
effect_sizes <- seq(0, max_effect_size, by = d) Running the chunk below generates the power curve.
# Calculates vector to hold power values
powers <- numeric(51)
# Loop through each effect size to calculate power
for (i in 1:51) {
effect_size <- effect_sizes[i]
power_calculation <- power_function(effect_size, standard_error, df, alpha)
powers[i] <- power_calculation
}
# Generate power curve data
power_data <- power_curve_function(max_effect_size, standard_error, df, alpha)
# Plot power curve
ggplot(power_data, aes(x = EffectSize, y = Power)) +
geom_line() +
labs(title = "Power Curve", x = "Effect Size", y = "Power") +
theme_minimal()
# This shows the table of power values for each effect size
View(power_data)The power curve is given below.
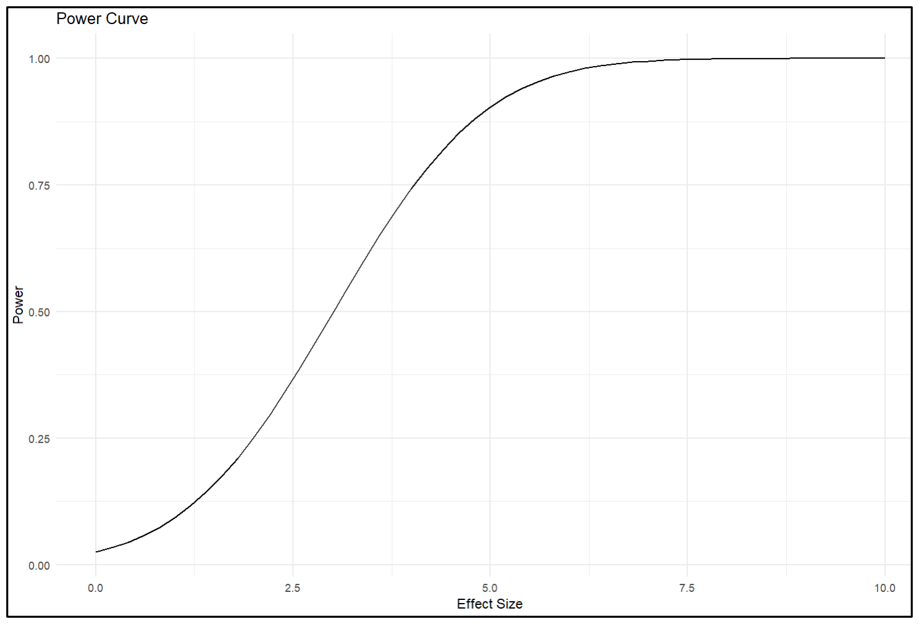
The last line of the chunk produces a dataframe that lists all the effect size-power value pairs. From there one can see that given a standard error of 1.5, the associated regression equation has an 80% probability of producing a statistically significant estimate when the effect size = 4.3.
The code above allows one to calculate power values and power curves for one’s own research. But perhaps its greatest value is that it allows one to conduct post hoc power analyses of estimated effects from other studies. All one needs to supply the programs is the standard error of the estimated effect and the associated degrees of freedom.
Limitation. The performance of the SE-ES method depends on the nature of the data and the type of estimator used for estimation. We found that it performed well when estimating linear models with clustered errors. However, one should be careful in applying the method to settings that are different from those investigated in our experiments. Accordingly, good practice would customize Tian et al.’s (2024) Monte Carlo simulations to see if the results carry over to data environments that represent the data at hand. To facilitate that, we have provided the respective codes and posted them at OSF here.
NOTE: Bob Reed is Professor of Economics and the Director of UCMeta at the University of Canterbury. He can be reached at bob.reed@canterbury.ac.nz.
REFERENCE
Tian, J., Coupé, T., Khatua, S., Reed, W. R., & Wood, B. D. K. (2024). Power to the researchers: Calculating power after estimation. Review of Development Economics, 1–35. https://doi.org/10.1111/rode.13130
COUPÉ: Why You Should Use Quarto to Make Your Papers More Replicable (and Your Life Easier!)
An important part of writing a paper is polishing the paper. You start with a first draft but then you find small mistakes, things to add or to remove. Which leads to redoing the analysis and a second, third and fourth draft of the paper. And then you get comments at seminars and from referees, further increasing the number of re-analyses and re-writes.
An annoying part of this process is that whenever you update your code and get new results, you also need to update the numbers and tables in your draft paper. Reformatting the same MS Word table for the 5th time is indeed frustrating. But it is also bad for the replicability of papers as it’s so easy to update the wrong column of a table or forget to update a number.
When writing my latest paper on the long term impact of war on life satisfaction, I discovered how Quarto allows one to solve these problems by enabling one to create code and paper from one document. It’s like writing your whole paper, text and code in Stata; or it’s like writing your whole paper, text and code in MS Word. True, R Markdown allows this too, but Quarto makes the process easier as it has MS Word-like drop down menus so you need to know less coding, making the learning curve substantially easier!
Whenever I now update the code for my latest paper, the text version gets updated automatically since every number and every table in the text is linked directly to the code! People who want to replicate the paper will also waste less time finding where in the code is the bit for table 5 from the paper, as the text is wrapped around the code so the code for table 5 is next to the text for table 5.
And there’s more! The R folder that has your code and datasets can easily be linked to Github so no more need to upload replication files to OSF or Harvard Dataverse!
And did I tell you documents in Quarto can be printed as pdf or word, and even html so you can publish your paper as a website: click here for an example.
How cool is that!
And did I tell you that you can use Quarto to create slides that are nicer than PPT and that can be linked directly to the code, so updating the code also means updating the numbers and tables in the slides?
Now I realize that, for the older reader, the cost of investing in R and Quarto might be prohibitive. But for the younger generation, there can only be one advice: drop Stata, drop Word, go for the free software that will make your life easier and science more replicable!
Tom Coupé is a Professor of Economics at the University of Canterbury, New Zealand. He can be contacted at tom.coupe@canterbury.ac.nz.
AoI*: “The Robustness Reproducibility of the American Economic Review” by Campbell et al. (2024)
[*AoI = “Articles of Interest” is a feature of TRN where we report abstracts of recent research related to replication and research integrity.]
ABSTRACT (taken from the article)
“We estimate the robustness reproducibility of key results from 17 non-experimental AER papers published in 2013 (8 papers) and 2022/23 (9 papers). We find that many of the results are not robust, with no improvement over time. The fraction of significant robustness tests (p<0.05) varies between 17% and 88% across the papers with a mean of 46%. The mean relative t/z-value of the robustness tests varies between 35% and 87% with a mean of 63%, suggesting selective reporting of analytical specifications that exaggerate statistical significance. A sample of economists (n=359) overestimates robustness reproducibility, but predictions are correlated with observed reproducibility.”
REFERENCE
COUPÉ: Why You Should Add a Specification Curve Analysis to Your Replications – and All Your Papers!
When making a conclusion based on a regression, we typically need to assume that the specification we use is the ‘correct’ specification. That is, we include the right control variables, use the right estimation technique, apply the right standard errors, etc. Unfortunately, most of the time theory doesn’t provide us with much guidance about what is the correct specification. To address such ‘model uncertainty’, many papers include robustness checks that show that conclusions remain the same whatever changes one makes to the main specification.
While when reading published papers, it’s rare to see specifications that do not support the main conclusions of a paper, many people who analyse data themselves quickly realize regression results often are much more fragile than what the published literature seems to suggest. For some, this even might lead to existential questions like “Why do I never get clean results, while everybody else does?”.
The recent literature based on ‘many-analyst’ projects confirms however that when different researchers are given the same research question and the same dataset, they often will come to different conclusions. Sometimes you can even observe such many-analyst project in real life: in a recent paper, my co-authors and I replicate several published papers that all use data from the same “Life in Transition Survey’ to estimate the long-term impact of war on life satisfaction. But while one paper concludes that there is a positive and significant effect, another concludes that there is a negative and significant effect, while a third one concludes there is no significant effect.
Interestingly, we can replicate the findings of these three papers so these differing findings cannot be explained by coding errors. Instead, it’s how these authors choose to specify their model that drove these differing results.
To illustrate the impact of specification choices on outcomes we use the specr R-package. To use specr, you indicate what are reasonable choices for your dependent variable, for your independent variable of interest, for your control variables, for your estimation model and for your sample restrictions. The general format is given below.
After specifying this snippet of code, specr will run all possible combinations and present them in two easy-to-understand graphs. For example, in our paper, we used 2 dependent variables (life satisfaction on a scale from 1-10 and life satisfaction on a scale from 1 to 5), one main variable of interest (injured or having relatives injured or killed during World War II), 5 models (based on how fixed effects and clusters were defined in 5 different published papers), 8 sets of controls (basic controls, additional war variables, income variables, other additional controls, etc.) and 4 datasets (the full dataset, respondents under 65 years old, those living in countries heavily affected by World War II, and under 65s living in heavily affected countries). This gave a total of 320 regression specifications.
The first graph produced by specr plots the specification curve, a curve showing all estimates of impact of the variable-of-interest on the outcome, and the standard errors, ordered from smallest to largest, giving an idea of the extent to which model uncertainty affects outcomes.
In the case of our paper, the specification curve showed a wide range of estimates of the impact of experiencing war on life satisfaction (from -0.5 to +0.25 on a scale of 1 to 5/10), with negative estimates often being significant (significant estimates are in red, grey is insignificant).
The second graph shows estimates by each specification-choice, illustrating what drives the heterogeneity in outcomes. In the case of our paper, we found that from the moment we controlled for a measure of income the estimate of war on life satisfaction became less negative and insignificant!
Given the potential importance of choices the researchers make on outcomes, it makes sense, when replicating a paper, to not just exactly replicating the authors specifications. Robustness checks in papers typically check how changing the specification in one dimension affects the outcome. A specification curve, however, allows to illustrate what happens if we look at all possible combinations of the robustness checks done in a paper. Moreover, programs like specr allow to easily check what happens if one adds other variables, include fixed effects or clusters at different level of aggregation, or restricts the sample in this or that way. In other words, you can illustrate the effects of model uncertainty in a much more comprehensive way than is typically done in a paper.
And why restrict this to replication papers only? Why not add a comprehensive specification curve to all your papers, showing the true extent of robustness in your own analysis too? In the process, you will perform a great service to many researchers, showing that they are not the only one getting estimates that are all over the place; and help science, by providing a more accurate picture of how sure we can be about what we know and what we do not know.
Tom Coupé is a Professor of Economics at the University of Canterbury, New Zealand. He can be contacted at tom.coupe@canterbury.ac.nz.
AoI*: “Mass Reproducibility and Replicability: A New Hope” by Brodeur et al. (2024)
[*AoI = “Articles of Interest” is a feature of TRN where we report abstracts of recent research related to replication and research integrity.]
ABSTRACT (taken from the article)
“This study pushes our understanding of research reliability by producing and replicating claims from 110 papers in leading economic and political science journals. The analysis involves com- putational reproducibility checks and robustness assessments. It reveals several patterns. First, we uncover a high rate of fully computationally reproducible results (over 85%). Second, excluding minor issues like missing packages or broken pathways, we uncover coding errors for about 25% of studies, with some studies containing multiple errors. Third, we test the robustness of the results to 5,511 re-analyses. We find a robustness reproducibility of about 70%. Robustness reproducibility rates are relatively higher for re-analyses that introduce new data and lower for re-analyses that change the sample or the definition of the dependent variable. Fourth, 52% of re-analysis effect size estimates are smaller than the original published estimates and the average statistical significance of a re-analysis is 77% of the original. Lastly, we rely on six teams of re- searchers working independently to answer eight additional research questions on the determinants of robustness reproducibility. Most teams find a negative relationship between replicators’ experience and reproducibility, while finding no relationship between reproducibility and the provision of intermediate or even raw data combined with the necessary cleaning codes.”
REFERENCE
WESSELBAUM: JCRE – An Outlet for Your Replications
Posted on by replicationnetwork
Leave a Comment
Replication studies play a crucial role in economics by ensuring the reliability, validity, and robustness of research findings. In an era where policy decisions and societal interventions heavily rely on economic research, the ability to replicate and validate research findings is important for making informed decisions and advancing knowledge. Replications in economics became more mainstream after the 2016 influential paper by Colin Camerer, Anna Dreber, and others published in Science. This paper replicated 18 studies from the AER and QJE published between 2011 and 2014. In only 61% (11 out of 18) of these, the replication found a significant effect in the same direction as in the original study.
Replication studies serve as a cornerstone of scientific integrity and transparency. Economics, like other empirical sciences, relies on data-driven analysis to draw conclusions about complex economic phenomena. However, the validity of these conclusions can often be challenged due to various factors such as data limitations, methodological choices, or even unintentional errors. By replicating papers, researchers can verify whether the original findings hold under different conditions, datasets, or methodologies. This process not only enhances the credibility of the research but also fosters trust.
Replications contribute to the cumulative nature of knowledge. Many economic theories and empirical results build upon earlier findings. However, the reliability of these findings can sometimes be uncertain, especially when they are based on limited samples or specific contexts. Replication studies allow researchers to confirm whether the findings are generalizable across different populations, time periods, or geographical regions. This cumulative process helps in refining theories, identifying boundaries, and uncovering inconsistencies that may require further investigation.
Additionally, replication studies encourage openness and collaboration within the economics community. They promote constructive dialogue among researchers about the strengths and limitations of different approaches and methodologies. By openly discussing replication efforts and their outcomes, we can collectively enhance research practices, improve data transparency, and foster a culture of quality assurance in economic research.
While some Journals (for example the Journal of Applied Econometrics, JPE: Micro, JESA, or Empirical Economics) publish replication studies, the new journal “Journal of Comments and Replications in Economics” (JCRE) aims to be the premier outlet for articles that comment on or replicate previously published articles.
Because many journals are reluctant to publish comments and replications, JCRE was founded to provide an outlet for research that explores whether published results are correct, robust, and/or generalizable and to publish replications defined as any study that directly addresses the reliability of a specific claim from a previously published study.
The editorial board of JCRE consists of W. Robert Reed (University of Canterbury), Marianne Saam (University of Hamburg), and myself (University of Otago). As editors, we are supported by the Leibniz Information Centre for Economics (ZBW) and the German Research Foundation (DFG).
Our advisory board consists of the following outstanding scholars: David Autor (MIT), Anna Dreber Almenberg (Stockholm School of Economics), Richard Easterlin (USC), Edward Leamer (UCLA), David Roodman (Open Philanthropy), and Jeffrey Wooldridge (MSU).
In conclusion, replication studies are indispensable in economics for several compelling reasons: they uphold scientific rigor and transparency, contribute to the cumulative advancement of knowledge, help identify biases and flaws in research, and promote openness and collaboration among researchers. We believe that with the increase in the availability of large data sets, the advancements in computer power, and the development of new econometric tools, the importance of replicating and validating research findings will only grow. To this end, we invite you to submit your replication studies to the JCRE and promote the Journal in your networks and among your students.
For more information about JCRE, click here.
Dennis Wesselbaum is Associate Professor of Economics at the University of Otago in New Zealand, and Co-Editor of the Journal of Comments and Replications in Economics (JCRE). He can be contacted at dennis.wesselbaum@otago.ac.nz.
Category: GUEST BLOGS Tags: Comments, economics, Journal, Journal policies, Publication, replications